Gradient Minimization is a force based approach for energy minimization. In this method forces and torques are calculated from continuously differentiable potential functions. These functions are Cubic Splines extrapolated from knowledge based potentials. Each potential function depends on distances or angles and can therefore be converted into forces and torques by deriving it. The resulting forces and torques are converted into translations, rotations and bendings in the XYZ coordinate plane of the secondary structure elements (SSEs).
Preliminary Data:
The prototype implementation of Gradient Minimization enabled us to increase the quality of our models as well as implement bending of the SSEs. We measured the quality by superimposing the native structure from the Protein Data Bank and calculating the RMSD. By applying Gradient Minimization we could decrease the RMSD and achieve more native-like (φ, ψ) angles.
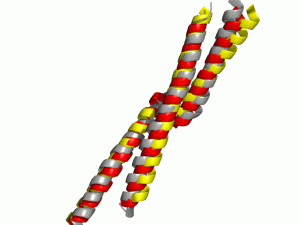
Comparison of the native structure (grey) and de novo predicted models with (red) and without (yellow) Gradient Minimization post processing. By using Gradient Minimization more native like (φ, ψ) angles could be achieved.
Expected Outcome and Interpretation:
We expect to produce more native-like structures by applying the Gradient Minimization technique. Our results will be evaluated by comparing with a benchmark set of native structures from the Protein Data Bank based on the RMSD score as well as the (φ, ψ) angles.
Challenges and Alternative Approaches:
The transformations calculated by the Gradient Minimization technique move the SSEs along the direction with the steepest slope of energy. Therefore it is possible to get stuck in a local energy minimum. To avoid this problem, we can combine Gradient Minimization with Simulated Annealing.
Alumni Project Members: Axel Fischer
