Despite improvements on both experimental techniques and computational prediction methods for small and medium sized proteins, structure elucidation and prediction for larger proteins remains a major challenge. We are developing a structure prediction algorithm that incorporates data of various experimental techniques but also to be used as a standalone tool. The algorithm utilizes a novel sampling technique and employs the flexible combination of empirical and experimental scores.The project consists of four parts:
a) optimization of secondary structure prediction,
b) a Monte-Carlo search algorithm based on secondary structure elements,
c) deriving empirical scoring functions from the Protein Data Bank (PDB),
d) translation of experimental information
a) Optimization of secondary structure prediction
There are many secondary structure prediction methods available, both for soluble and membrane proteins. Furthermore, consensus methods have proven to be the most successful. Soluble methods are not reliable when building a general prediction method because they do not address potential membrane spanning regions of a protein. Concomitantly, if there are long stretches of soluble protein between transmembrane segments membrane prediction methods are inadequate. Therefore, we developed an algorithm that reliably merges soluble and membrane predictions. If available, experimental information, such as chemical shift index for C atoms, can be incorporated. Figure 2 shows an example of the scheme we have developed for diacyl glycerol kinase (DAGK). The prediction methods used for soluble proteins are: JUFO, SAM, PSIPRED. For membrane helices: CONPRED, TMMOD. For membrane strands: PROFTMB, HMMB2TMPRED. Furthermore, we use the hydrophobicity scales of Whimley & White, and Engelman, Seitz and Goldman. We are determining an optimized set of weights within this consensus scheme.
b) A Monte-Carlo search algorithm based on secondary structure elements
While the backbone geometry of a protein determines the overall fold, it is extremely computationally expensive to search the conformational space using backbone angles. Yet, cutting off loop regions and focusing on ideal secondary structure elements allows one to scan the conformational space of larger proteins sufficiently. This is justified because the loop regions are more functionally rather than structurally relevant. Reducing the representation of the amino acids to und atoms (and deriving according potentials) further reduces complexity and computational costs.
While computation time and therefore explorable conformational space improves, the ability to distinguish native from non-native conformations decreases. That means the search will not lead to a single resulting structure, but to an ensemble of conformations. These conformations are further selected and refined by adding loops and side-chains with Rosetta.
We use a Monte-Carlo based search with simulated annealing, which has shown to outperform more systematic approaches like gradient-based methods, due to the complexity and ruggedness of the conformational space.
Possible Monte-Carlo steps are:
1) adding a new structure element,
2) moving a structure element,
3) bending a structure element,
4) adding or removing residues of a structure element.
**Step 3 involves breaking long structure elements into short ideal ones and moving them in a pseudo-bending like fashion.
**Step 4 counterbalances possible over- or underpredictions from the secondary structure consensus.
c) Deriving empirical scoring functions from the Protein Data Bank (PDB)
Statistical potentials are strikingly more efficient in describing molecular interactions than first-principle potentials at this stage. We derive statistical potentials that include amino-acid pair scores, secondary structure element packing and solvation terms. These will also be derived for membrane proteins. Another scoring scheme predicts the probability of two sequence windows to be in contact, based on artificial neural networks.
(links: contact prediction , scores )
d) Translation of experimental information into scoring functions
Incorporation of experimental constraints leads to structure prediction with the highest resolution and confidence.Even a relatively small number of constraints allows one to drastically reduce the number of resulting structures and to improve resolution. We translate experimental information into scoring functions, which can be used during the Monte-Carlo search. They score the agreement of a conformation with the data. This setup allows one to include several data sets from different techniques in parallel and exploit low-resolution data. Established collaborations provide data from X-Ray Cristallography, NMR and Cryo-EM.
(link: density maps )
Figure 2 – Schematics of the secondary structure prediction consensus
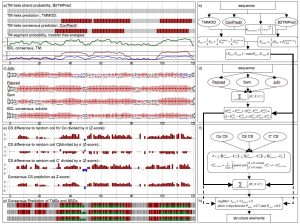
The implementation offers a very flexible treatment of both scoring scheme and search-objects. Each Monte-Carlo move is related to a decision tree, which picks moves according to assigned probabilities. This gives a high level of flexibility for the search algorithm as well, because both general ( i.e. free rotation and translation) and more specific moves ( i.e. adding a new structure element to an existing model in the membrane plane) are allowed and biased by probability. It is written as a C++ class library and is part of the BCL ( BioChemical Library), commonly developed in our lab.
Alumni Project Members: Elizabeth Durham, Rene Staritzbichler, Nils Woetzel, Mert Karakas, Nathan alexander, Bian Li, Axel Fischer, Marcin J. Skwark
